大垣市波須　総合学習塾　小学生・中学生・高校生　学習支援

こんにちは。河村学習塾波須校の園部です。昨日に引き続き、 大学入学共通テスト 対策について。

共通テスト予想問題を使って成績をあげるためのポイントは2つです。

一つ目は、時間を短くして対策をすること。

本番は焦りや緊張でなかなか本来の実力を出すことが出来ない環境です。

少しでも計算ミスや思い違いで解けない問題があるとなおさら悪いループにはまってしまいます。

こうならないためにも、本番の精神的余裕を少しでも増やすため規定の時間の9割で解いておきましょう！

,b>二つ目はまとめノートを作ること。

共通テスト試験で落としてしまった問題はどのような形であれ、基礎の穴であることは間違いないです。

こうした基礎の穴を軽視せずに、こうした穴を埋めていく作業が大事です。

そのために使えるのがまとめノート。

共通テスト試験においてやりがちなミスや抜けていた基礎知識をノートにまとめておき、直前期の総仕上げに役立てましょう。

こんにちは。河村学習塾波須校の園部です。今日は 大学入学共通テスト 対策をいつから始めるべきか、というテーマです。

結論から言えば、11月中旬頃から本格的に共通テスト対策に取り組み始めるべきだと言えるでしょう。

受験生の基本的な勉強の流れとしては、夏までに基礎を固め、秋頃から応用問題や大学個別試験への対策を進め、冬になってだんだんと共通テストに切り替えた後、共通テストに挑み、各大学の対策・本番へと進んでいく形です。

従って、11月中旬ごろからジワジワと予想問題を解き始め、12月になると本番形式での演習を行っていく形になるでしょう。

ただ、意識すべきは、共通テストに必要以上の時間を割かないこと。

共通テストはあくまで基礎的な出題ですし、どれだけ良く出来たとしても共通テストの結果だけで大学に合格できるわけではありません。

従って、9月や10月など、各大学の過去問対策をするべき時に、共通テスト対策をやるのはあまりよくないケースだと言えます。

もちろん、基礎固めの延長として共通テストは非常に良い問題を出していますので、そういった意味での問題演習に使うのは賢い選択だと言えます。

こうした場合は、予想問題を使用するのではなく、形式がほぼ変わらないセンター試験の過去問を使用すると良いでしょう。

こんにちは。河村学習塾波須校の園部です。今日は 大学入学共通テスト について。

大学入学共通テスト は、10月8日で出願も終了しました。

令和3年1月16日(土)、17日(日)に行われる共通テストまで、

残り１４週間です

週に１時間しか勉強していない科目があったとしたら、

その科目は残り15時間で完成させなければいけません。

どの科目もやらないといけないことは山積みなので、

この時期は本当に時間が足りなくなって、

受験生達は焦ります

これまでの共通テスト模試もプレテストを参考に作られた程度のものでしたが、

・実際のところどのレベルの問題がでるかわからない
・国語は書き取りが無くなった分を何で補填されるのかもよくわからない
・当初の発表通り、平均点4割でつくられてくるのだろうか・・・

などといろいろ考えたら、

模試も難易度の高いものを作らざるを得ないのでしょう。

思考力を問うというか。。。難易度を問うというか。。。

作る方も、解く方も苦戦しているような感じです。

実際、学習内容の根本を理解していれば解ける問題が多いです。

まだ表面的な過去問の勉強で止まっている多くの生徒には難しいでしょう。

未知の共通テスト対策・・・

私のお薦めとしては、

過去問や問題集（問題集も過去問なので）にとらわれすぎずに、

『参考書』を読んで

知識をしっかりとことばで理解すること。

これをお薦めしたいです。

こんにちは。河村学習塾波須校の園部です。昨日更新した 大学推薦入試 についてのブログをご覧になった方から、 大学推薦入試 の種類についてお問い合わせがあったので、まとめてみました。

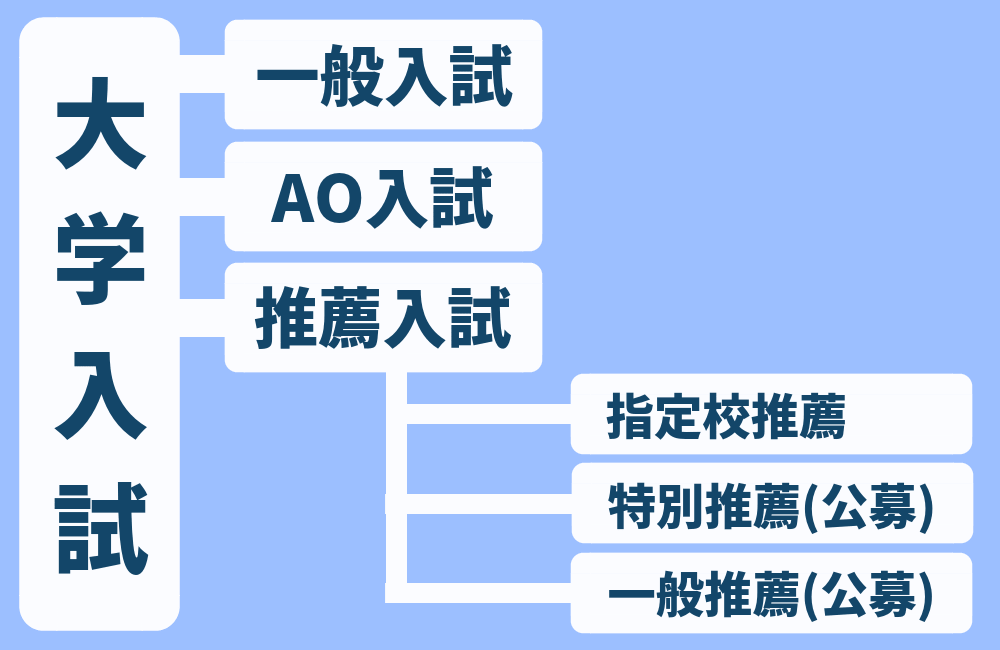
大学入試には、大きく分けて一般入試と推薦入試があります。

推薦入試には

• 「指定校制推薦」
• 「公募制特別推薦」
• 「公募制一般推薦」

の３種類があります。

１．指定校制推薦

大学が特定の高校を指定して行う推薦入試です。

高校における成績や部活動などを評価する校内選考の結果受験生を決定し、場合によっては、受験者数も各高校に事前に割り振られます。

そして、「よほどのことがない限り合格する」という特徴があります。

基本的に専願ですので、合格した場合は必ず入学することが前提です。

かつて、どうしても辞退したいという事例はありましたが、その高校の指定校推薦枠が一枠減らされたという事例もあります。

出願する場合は慎重にしましょう。

 ２．公募制推薦

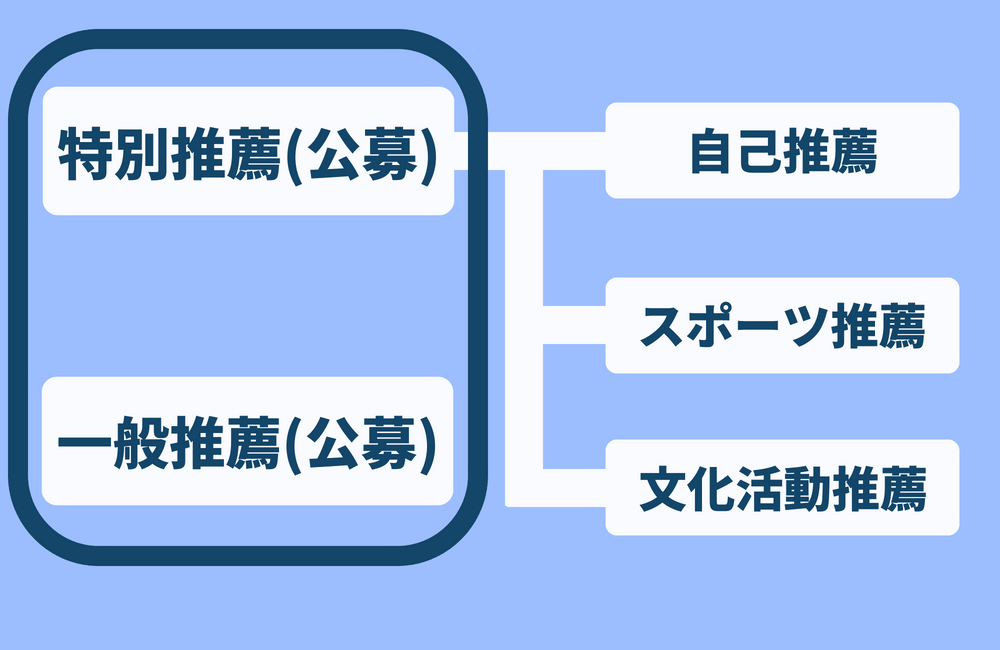
（１）公募制特別推薦

公募制特別推薦には

• 「自己推薦」
• 「スポーツ推薦」
• 「文化活動推薦」

の主に３種類があります。

出願に際して成績基準が設けられていない場合もあり、主にスポーツ活動や文化活動の成績が評価される推薦入試の形式です。

また、委員会活動やボランティア活動も評価の対象となります。

「学業成績以外に誇れるものがある！」という学生におすすめの入試形式です。

ちなみに、受けても落ちる可能性は十分にあります。

（２）公募制一般推薦

各大学が募集要項で示している出願資格を満たし、出身学校長の推薦を得ることができれば誰でも出願することができる推薦入試です。

出願資格に評定平均が含まれることが多いです。

基本的には合格したら必ず入学することが前提ですので、注意してください。

ちなみに、受けても落ちる可能性は十分にあります。

３．AO入試と推薦入試の共通点と相違点

（１）AO入試と推薦入試の共通点

共通点は、選考方法が書類審査・小論文・面接中心であることです。

これに、集団討論などが追加されることがあります。

どの選考方法を用いるかは、各大学の方針によって異なります。

このことから、AO入試と公募制一般推薦入試の選考方法が類似していることがわかります。

また、どちらの試験も出身高校から出される「調査書」が重要な判断材料の一つとなります。

（２）AO入試と推薦入試の相違点

一番の相違点は、大半のAO入試には学校長からの推薦が不要だということです。

したがって、公募制推薦と比較すると、AO入試は自己プレゼン能力がより必要とされます。

それぞれの特徴をつかみ、自分に合う入試を選択していってください。

こんにちは。河村学習塾波須校の園部です。本日は 大学推薦入試 について。

いよいよ10月に入り、今年度の大学入試関係も指定校推薦・総合型選抜（旧AO）系の入試など募集要項が決まり始めているようです。

やはり今年度は新型コロナウィルス感染症の影響がかなり出ているようです。

ある大学では指定校推薦に関しては予定していた面接試験は免除、書類選考のみでの選抜へ。

またある大学の総合型選抜（旧AO）入試ではもともと発表していた試験日程を遅らせるなど大学側もいろいろ変更を余儀なくされているようです。

こういった対応は各大学によってまちまちですので、自分が受験を考えている大学の変更点などは大学の公式HPなどでまめに最新情報をチェックするようにしていくことが大切です。

受験生たち、学校のテスト…受験のこと…いろいろ大変だと思うけど、頑張ってください！

こんにちは。河村学習塾波須校の園部です。今日は関西大学の 数学 の入試問題から。

連立方程式
x+(a−1)y=−1
ax+(a+3)y=1
について、以下の問いに答えよ。
(1)解が存在しないときのaの値を求めよ。
(2)解が無数に存在するときのaの値を求めよ。

ヒント、着眼点
中学校的な方法でこの問題を解くことができます。
中学校で1次関数を習います。その単元で、連立方程式の解と2つの式が表す直線の交点の座標が対応していると習います。
そこで、この問題を連立方程式としてではなく、2つの1次関数とグラフの問題としてとらえてみましょう。
さて、解が存在しない、無数に存在するとは1次関数のグラフ上ではどういう風に言い換えることができるのでしょうか。
解答
(1) 3
(2) -1

解説
連立方程式の解と2つの式が表す直線の交点の座標は同じということから「解が存在しない」「無数に存在する」をいいかえると、

解が存在しない→2つの直線の交点がない→2直線が平行で重なっていない
解が無数に存在する→2つの直線の交点が無数にある→2直線が平行で完全に重なっている
となります。

x+(a−1)y=−1 (1)
ax+(a+3)y=1 (2)
それぞれyについて解いて、
y=−x/(a−1)−1/(a−1) (1)
y=−ax/(a+3)+1/(a+3) (2)
2直線が平行になるということは、傾きが等しいということなので、
−1/(a−1)=−a/(a+3)
これを解けばa=3,a=−1 が得られます。そして、それぞれのaの値のとき切片が異なれば2直線は平行で交点を持たず、等しくなれば2直線は完全に重なります。
a=3 のとき、
y=−12x−12 (1)
y=−12x+16 (2)
より2直線は平行で交点を持たない。

a=−1 のとき、
y=12x+12 (1)
y=12x+12 (2)
より2直線は完全に重なる。

中学生で習ったグラフと式の性質を覚えているかどうかがポイントでした。係数比較の感覚も併せて覚えておきましょう。

こんにちは。河村学習塾波須校の園部です。今日は明治大学の 数学 の入試問題から。

高校で習う公式を使っていますが、式自体は難しくないため、中学生でも解けるような問題です。

■　問題
(1) 50以下の自然数で、2の倍数か5の倍数であるものの個数を求めよ。
(2) 50以下の自然数で、2の倍数か5の倍数であるものの総和を求めよ。
(3) 1/50から50/50までの50個の分数のうち、既約分数の総和を求めよ。
※既約分数とは、これ以上約分できない分数のこと。

■　解答
(1)
1から50のうち2の倍数の個数は、50÷2=25より25個です。
1から50のうち5の倍数の個数は、50÷5=10より10個です。
ここで、答えは35とはならないことに注意しましょう。
上でカウントした35個の数の中には、2の倍数と5の倍数とで2回重複してカウントされたものが混ざっています。
2の倍数と5の倍数で両方登場する数は最小公倍数の10の倍数の数なので、50÷10=5個あります。よって35-5=30個

(2)
1+2+3+⋯+(n-2)+(n-1)+n=n(n+1)/2を利用してみましょう。
2の倍数の総和は、
2+4+6+…+48+50=2(1+2+3+…+24+25)=2×(25×26)/2=650
5の倍数の総和は、
5+10+15+…+45+50=5(1+2+3+…+10)=5×(10×11)/2=275
この2つを足すのみだと、先ほどと同様、10の倍数が2回足されてしまうので、
10の倍数の総和は、
10+20+30+40+50=150
よって650+275-150=775

(3)
1/50,2/50,,…,50/50
既約分数と約分できる分数にどんな違いがあるかを考えます。
約分できる分数は、分母が50=2×5×5であることから、分子が2か5で割り切れる、つまり分子が2の倍数か5の倍数であることが分かります。逆に、既約分数は分子が2でも5でも割り切れないもの、と言えます。そこで、
(1/50から50/50全ての総和)-(約分できる分数の総和)=(既約分数の総和)
で求めます。1/50から50/50全ての総和は、
1/50+2/50+3/50+⋯+50/50=(1+2+3+⋯+50)/50=(50×51/2)/50=1275/50=51/2
約分できる分数の総和は、分子の合計は(2)がそのまま使えるので、
775/50=31/2
よって、答えは51/2−31/2=10

補足1
x=1+2+3+……(n-2)+(n-1)+n…①と置いた時、右辺の項を逆順にすると
x=n+(n-1)+(n-2)+……+3+2+1となりますね。
この2式を足すと左辺は2x、右辺は各項がn+1となり、それがn個あるという式になります。
つまり2x=(n+1)×nとなり、両辺を2で割るとx=n(n+1)/2…②という式が得られます。
よって①②より、1+2+3+……(n-2)+(n-1)+n=n(n+1)/2となります。

補足2
「1からnのうちaかbで割り切れる数の個数」と言われたら、
(aで割れる個数)+(bで割れる個数)-(abの最小公倍数で割れる個数)
で求めるのが普通です。ぜひ覚えましょう。

例　1から100までの中で12でも18でも割り切れない数の個数を求めよ。
12か18で割り切れる個数を求めて、それを100から引いて求めます。
12で割り切れる個数は、100÷12=8…4より8個
18で割り切れる個数は、100÷18=5…10より5個
余分に数えている分は、12と18の最小公倍数の36の倍数だから、
100÷36=2…28より 2個
以上から、12か18で割り切れる個数は8+5-2=11個
よって答えは100-11=89個

こんにちは。河村学習塾波須校の園部です。本日は 岐阜女子高等学校 の説明会に行ってまいりました。

岐阜女子高等学校 は、普通科【文理科コース、一般コース（進学類型・美術類型）】、食物科を持つ私立高校です。

女子が過ごしやすい環境の構築や、自立心やリーダーシップが養われること、女子の特性に合わせた教育ができることなど、パンフレットに書かれているような内容よりもさらに踏み込んだ気概あふれる言葉から説明が始まりました。

こういった気持ちの伝わる説明会は、生徒が入学した後も安心できそうだと感じますね。

学科やコースなどに変更はありませんでしたが、奨学生に特別奨学生Aと特別奨学生Bが新設され、全部で5種類の奨学金形態となっています。

それぞれの出願基準や目安も伺っておりますが、こちらはHP等で公表できない情報となりますので、生徒および保護者様との面談の中でお伝えしていきます。

また修学支援金も昨年度から大きく増額となっているため、費用が随分抑えられるようになってきていることを改めて説明されていました。

進路に幅広い選択肢を得られるのはメリットだと考えているので、引き続き情報を集めていきます。

こんにちは。河村学習塾波須校の園部です。今日は2019年の法政大学の 数学 の入試問題から。

■　問題
1/x+1/y=2 とする。
(1) x+y=4 のとき、x²+y² の値を求めよ。
(2) x²+y²=4 のとき、x+y の値を求めよ。

■　解説

(1)
1/x+1/y=2 の両辺に xy をかけると、
x+y=2xy
を得る。
x+y=4であるから、
4=2xy
xy=2
すると、
x²+y²=(x+y)²−2xy=42−2×2=12

(2)
x+y=k とおくと、
x+y=2xy より2xy=k
x²+y²=4 より、
(x+y)²−2xy=4
k²−k=4
これを解いて、
k=1±√17/2
よって、
x+y=1±√17/2

いかがでしたでしょうか。 少し難易度の高い私立「高校」の入試でも十分あり得る問題です。
置き換えと平方完成による柔軟な対応力がポイントですね。是非挑戦してみてください。

こんにちは。河村学習塾波須校の園部です。今日は静岡大学の 数学 の入試問題から。

3桁の自然数の百の位の数をa、十の位の数をb、一の位の数をcとする。
(1) 10a+b-2cが7の倍数ならばもとの自然数は7の倍数であることを示せ。
(2) a≠b, a=cであるとき、もとの自然数が7の倍数となるようなaとbの組は何通りあるか。

■　解説
(1)
3桁の自然数は100a+10b+cを書ける。
10a+b-2cが7の倍数なので、nを整数として
10a+b-2c=7n
と書ける。このとき
100a+10b+c
=(70a+7b+7c)+(30a+3b-6c)
=7(10a+b+c)+3(10a+b-2c)
=7(10a+b+c)+21n
=7(10a+b+c+3n)
a,b,c,nは整数だから7(10a+b+c+3n)は7の倍数である。よってもとの自然数は7の倍数である。

100a+10b+c=(90a+9b+3c)+(10a+b-2c)としてもうまくいかず、7の倍数を作るために上のような一工夫をするのが少し思いつきにくいでしょうか。

(2)
(1)より、10a+b-2cが7の倍数となることを考えればよい。a=cより、
10a+b-2c=8a+b=7a+(a+b)
7aは7の倍数より、これが7の倍数となるのはa+bが7の倍数となるときで、a+b=7,14となるときであり、
(a,b)=(1,6), (2,5), (3,4), (4,3), (5,2), (6,1), (7,0), (5,9), (6,8), (8,6), (9,5)
の11通り。

(a,b)=(0,7) は3桁の自然数でなくなることに注意。
(a,b)=(7,7) はa≠bに反することに注意。

いかがでしたでしょうか。来週ももう少し紹介していこうと思います。